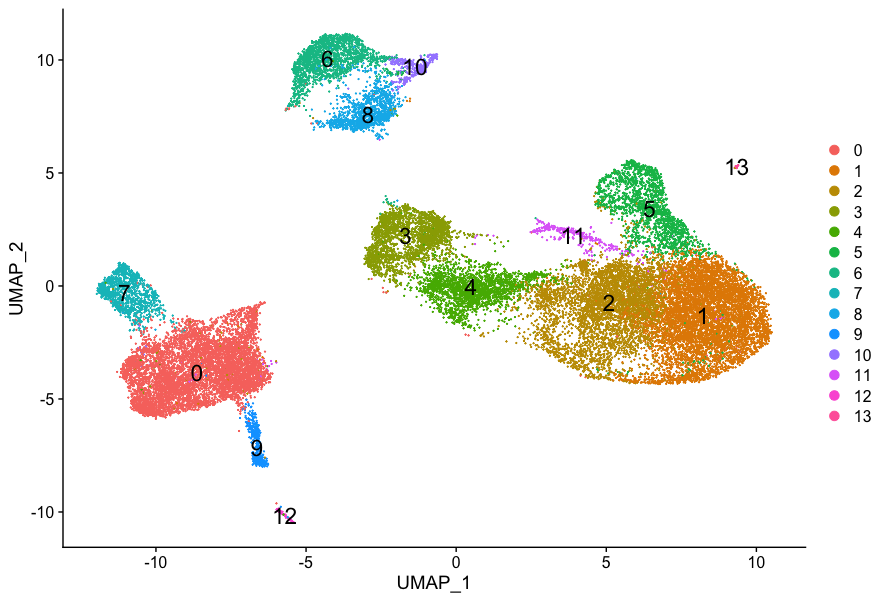
Umap Interpretation. The algorithm is founded on three assumptions about the data The data is uniformly distributed on Riemannian manifold; For each individual in a genetic dataset, UMAP identifies a pre-set number of nearest neighbours and represents distances to these neighbours as a weighted graph where the nearest neighbours are. Understanding UMAP Andy Coenen, Adam Pearce It provides a very general framework for approaching manifold learning and dimension reduction, but can also provide specific concrete realizations. Uniform Manifold Approximation and Projection (UMAP) is a dimension reduction technique that can be used for visualisation similarly to t-SNE, but also for general non-linear dimension reduction. The work highlights the use of UMAP for improved visualization and interpretation of single-cell data. The UMAP provides the ecologically meaningful interpretation of the results obtained..
Umap Interpretation. It provides a very general framework for approaching manifold learning and dimension reduction, but can also provide specific concrete realizations. Rather than seeking to provide a comprehensive solution that covers all possible plotting. UMAP is an algorithm for dimension reduction based on manifold learning techniques and ideas from topological data analysis. The work highlights the use of UMAP for improved visualization and interpretation of single-cell data. Input similarities are unimportant as they get binarized; only the kNN graph matters. Main The past decades have witnessed a large increment in the number of parameters. Umap Interpretation.
The algorithm is founded on three assumptions about the data The data is uniformly distributed on Riemannian manifold; For each individual in a genetic dataset, UMAP identifies a pre-set number of nearest neighbours and represents distances to these neighbours as a weighted graph where the nearest neighbours are.
The work highlights the use of UMAP for improved visualization and interpretation of single-cell data.
UMAP projection of the 1000 deep features of SEQC-NBt samples on the …
Single-cell RNA-seq: Clustering Analysis | Introduction to single-cell …
Interpretation of UMAP clustering data : r/bioinformatics
Example of 2D visualization after dimensionality reduction using UMAP …
UMAP visualization of the 56 subtrajectories, coloured by inferred …
Neural network interpretation. (a) A UMAP projection of the latent …
Creation of threads in a container of the UMAP platform | Download …
Mapping Chemical Space with UMAP
UMAP: Uniform Manifold Approximation and Projection for Dimension …
UMAP representation at the Mixed 5c Concatenated layer of the Inception …
Interpretation of WM pathological features used for disease …
Problem with UMAP visualization ยท Issue #2784 ยท satijalab/seurat ยท GitHub
Umap Interpretation. Main The past decades have witnessed a large increment in the number of parameters. The main difference between t-SNE and UMAP is the interpretation of the distance between objects or "clusters". Uniform Manifold Approximation and Projection (UMAP) is a dimension reduction technique that can be used for visualisation similarly to t-SNE, but also for general non-linear dimension reduction. The great dimensionality reduction algorithm in one video with a lot of visualizations and a. Since this is such a common use case the umap package now includes utility routines to make plotting UMAP results simple, and provide a number of ways to view and diagnose the results. Google PAIR Dimensionality reduction is a powerful tool for machine learning practitioners to visualize and understand large, high dimensional datasets.
Umap Interpretation.