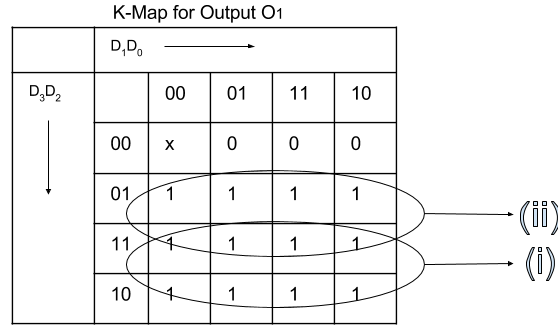
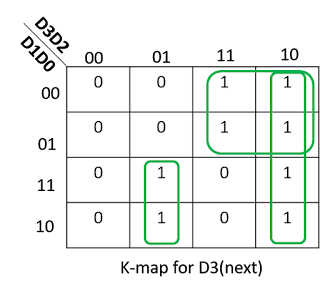
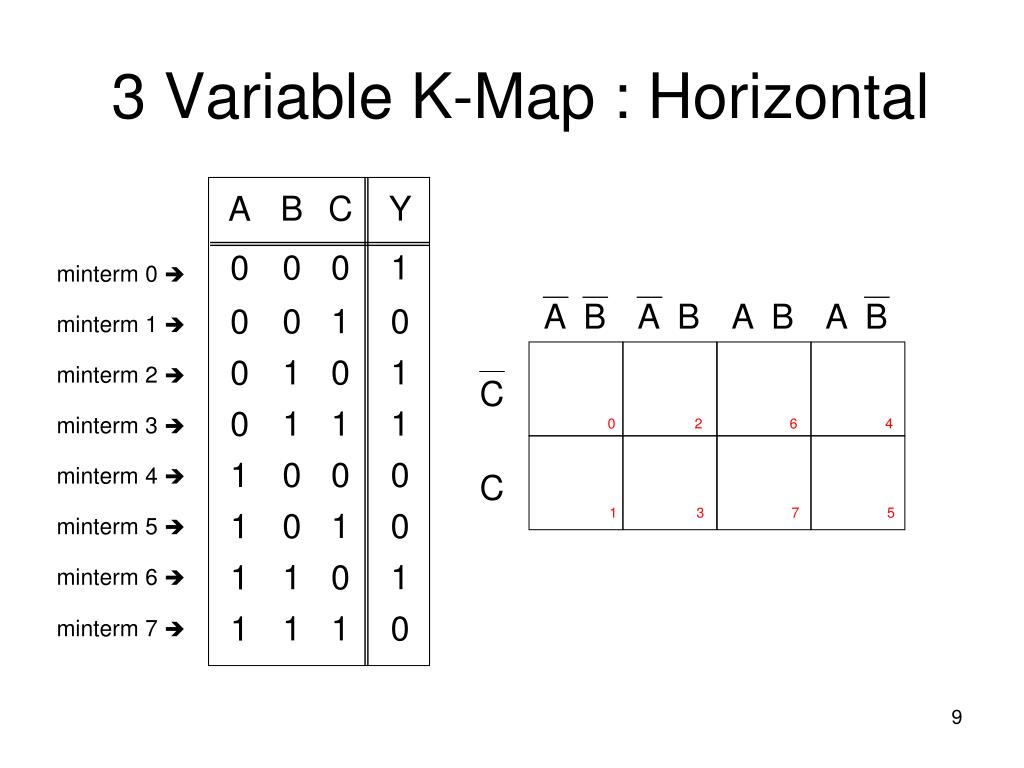
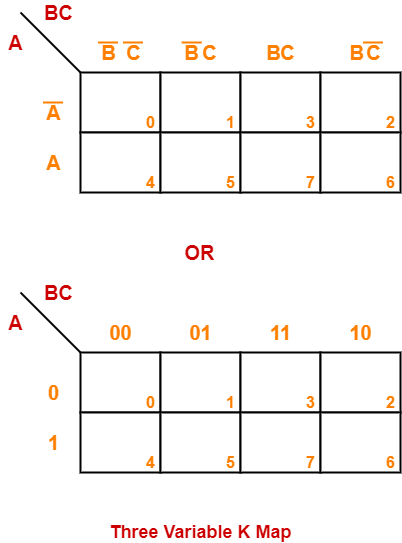
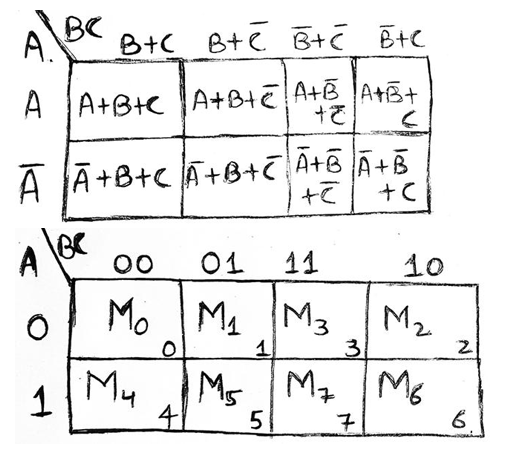
K Map In Discrete Mathematics. K-map is table like representation but it gives more information than TRUTH TABLE. A K-map in three variables is a rectangle divided into eight cells. It's used to simplify Boolean expressions where you have more than two variables. The Karnaugh map ( KM or K-map) is a method of simplifying Boolean algebra expressions. a.)Complete the truth table that describes a full adder: The Boolean function that adds two bits A, B, and a carry-in bit Cin to produce a sum bit S and a carry-out bit Cout. b.)Using Karnaugh maps find Boolean expressions that represent the sum function S and the carry-out function Cin. c.)Draw the circuit of the full adder. The cells represent the eight possible minterms in three variables. Two cells are said to be adjacent if the minterms that they represent differ in exactly one literal.
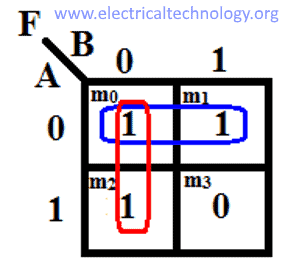
K Map In Discrete Mathematics. The Karnaugh map ( KM or K-map) is a method of simplifying Boolean algebra expressions. a.)Complete the truth table that describes a full adder: The Boolean function that adds two bits A, B, and a carry-in bit Cin to produce a sum bit S and a carry-out bit Cout. b.)Using Karnaugh maps find Boolean expressions that represent the sum function S and the carry-out function Cin. c.)Draw the circuit of the full adder. Two Variable K Map- Two variable K Map is drawn for a boolean expression consisting of two variables. In this lesson, we will introduce the concept of K-Maps with a simple, two-variable map. We want to know if it contains elements not associated with any element in the domain. Karnaugh Maps are quicker and easier to use than. One-to-one functions focus on the elements in the domain. K Map In Discrete Mathematics.
It's used to simplify Boolean expressions where you have more than two variables.
Onto functions focus on the codomain.
K Map Calculator With Steps
K Map or Karnaugh Map – Digital Electronics
UGC-NET Computer Science Topics: Priority Encoder
DESIGN PROBLEM : 4-bit increment by 2 circuit
K map Problems – YouTube
Karnaugh Maps (K-Map) | 1-6 Variables Simplification & Examples
25 3 Variable K Map – Maps Online For You
K Maps PPT | Gate Vidyalay
K-Map (Karnaugh Map) – GeeksforGeeks
K-Map (Karnaugh Map) – GeeksforGeeks
25 3 Variable K Map – Maps Online For You
PPT – K-Maps PowerPoint Presentation, free download – ID:1406594
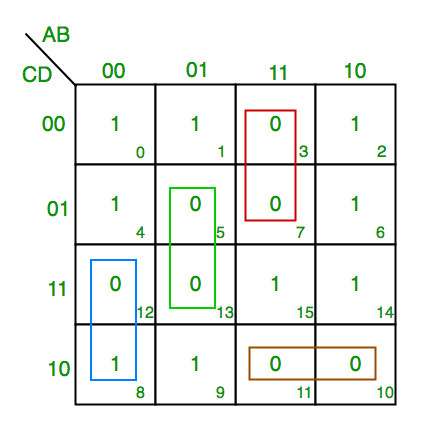
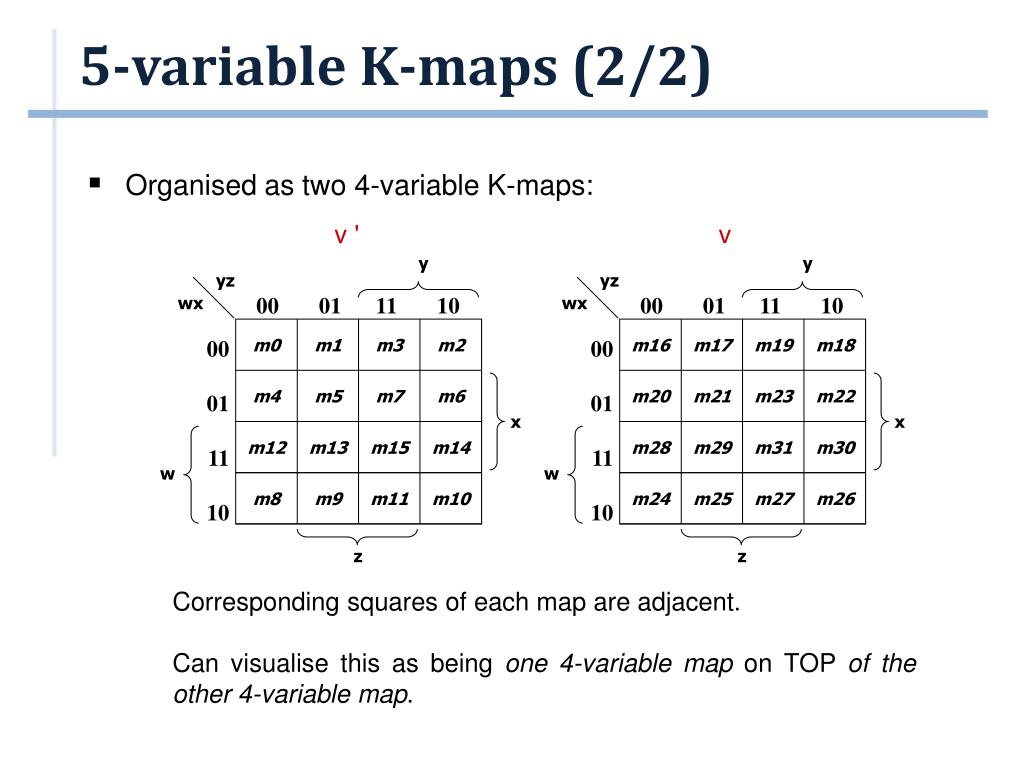
K Map In Discrete Mathematics. We do not want any two of them sharing a common image. Two Variable K Map- Two variable K Map is drawn for a boolean expression consisting of two variables. Use a K-map to find a minimal expansion as a Boolean sum of Boolean products of each of these functions in the variables w, x, y, and z. ๐Subscribe to our new channel:https://www.youtube.com/@varunainashots In many digital circuits and practical problems we need to find expression with minimu. The S-packing chromatic number of G is the smallest integer k such that G admits an S-packing k-coloring. Two cells are said to be adjacent if the minterms that they represent differ in exactly one literal. The Karnaugh map ( KM or K-map) is a method of simplifying Boolean algebra expressions. a.)Complete the truth table that describes a full adder: The Boolean function that adds two bits A, B, and a carry-in bit Cin to produce a sum bit S and a carry-out bit Cout. b.)Using Karnaugh maps find Boolean expressions that represent the sum function S and the carry-out function Cin. c.)Draw the circuit of the full adder.
K Map In Discrete Mathematics.